相互作用拓扑绝缘体中拓扑不变量的计算取得进展

卢仲毅 研究组 供稿 2016-06-08

 拓扑物质形态，如具有拓扑序的量子霍尔态以及拓扑绝缘体，是近年来凝聚态物理领域最大的进展之一。在拓扑绝缘体中加入电子之间的强关联相互作用，研究可能涌现的新的拓扑物态，以及拓扑物态之间由于相互作用驱动的拓扑相变，是人们关心的问题。前期拓扑绝缘体的理论和实验研究，主要集中于无相互作用或弱相互作用系统，而对于强关联电子系统中的拓扑相变和拓扑不变量的精确计算却付之阙如，并且往往存在把无相互作用系统中的拓扑不变量计算方法简单推广到相互作用系统中，造成概念和实践上的混乱等等现象。因此，如何正确计算相互作用电子系统中的拓扑不变量，探测相互作用驱动的拓扑相变和拓扑物态，是十分基础的问题。

中国人民大学博士研究生何院耀、邬汉青，教授卢仲毅，中国科学院物理研究所/北京凝聚态国家实验室T03组副研究员孟子杨组成的研究团队，在相互作用拓扑绝缘体中拓扑不变量的数值计算方面，开展了系统的工作，取得了进展。他们首先发展了计算相互作用电子系统的拓扑不变量的数值方法，并运用大规模量子蒙特卡洛计算在常见的拓扑绝缘体模型中进行了数值实现；然后，更有意思的是，他们找到并严格计算了几种相互作用驱动的、没有对称性自然破缺的拓扑量子相变，发现目前被大量使用的、通过单粒子格林函数计算拓扑不变量的方法对于这类拓扑相变完全失效，指出了现有的拓扑不变量理论，在向强关联电子系统拓展时，不能依靠单粒子格林函数来计算，而需要在集体激发中寻找系统的拓扑信息，澄清了理论上的混乱和误区。

如图1、图2所示，在上述研究工作的前半部分中，他们运用相互作用系统中的零频率单粒子格林函数，设计了准确计算Z2不变量和自旋陈数的计算方法。由于量子蒙特卡洛方法都是计算有限尺寸的系统，自旋陈数因为有限尺寸效应得到的都是非整数的结果，他们借鉴了团簇动力学平均场理论中的周期化方案，提出一种针对周期函数的差值方案，有效地克服了自旋陈数结果的有限尺寸效应，使得即使对于有限尺寸系统也能计算得到整数化的自旋陈数。

如图3、图4所示，在上述研究工作的后半部分中，他们使用自己发展的计算自旋陈数的方法探测了一些相互作用驱动的、没有对称性自发破缺的拓扑量子相变，发现在某些直积态（拓扑平庸态，自旋霍尔电导率为0）系统中，数值计算得到了非零的自旋陈数。显然，这个非零自旋陈数并不对应物理上可观测的自旋霍尔电导率，因为后者在直积态为0。这说明用单粒子格林函数构造的自旋陈数在这样的直积态中失效，而他们发现这样的直积态的共同特点是没有无相互作用的绝缘体能与之不经历相变地、没有对称性破缺地连接。

这样现象背后的原因在于，在无相互作用电子系统中，拓扑不变量有确定的物理意义，即对应系统可观测的（自旋）霍尔电导率。但是在相互作用电子系统中，用单粒子格林函数构造的拓扑不变量并不对应于系统中真实的（自旋）霍尔电导率。长期以来人们一直有这样的怀疑，但是并没有找到真正的例子。卢仲毅和孟子杨团队的研究工作首次从数值的角度通过严格的数值计算给出了用单粒子格林函数构造的拓扑不变量在相互作用拓扑绝缘体中失效的证据，给出了用单粒子格林函数构造的拓扑不变量的适用条件，指出了在一大类相互作用的拓扑物态中需要在集体激发中寻找系统的拓扑信息。

从现有的研究工作来看，相互作用电子系统中拓扑不变量的构造和分类还远不完备，需要使用什么样的拓扑不变量来地描述相互作用量子相的拓扑性质是正在快速发展的领域。卢仲毅和孟子杨团队这一系列工作推动了相互作用拓扑物态中拓扑不变量的数值计算和拓扑相变的研究。该工作分被为两篇较长篇幅的文章，连载地发表在Physical Review B（Phys. Rev. B 93, 195163 (2016) 和 Phys. Rev. B 93, 195164 (2016)）。

上述工作得到了国家青年千人计划（孟子杨），国家自然科学基金和国家基础科学研究计划（何院耀、邬汉青、孟子杨、卢仲毅）的支持。量子蒙特卡洛模拟所需的大规模的并行计算在中国科学院物理研究所量子科学模拟中心，中国人民大学物理系高性能并行计算物理实验室，天津国家超算中心天河1号、广州国家超算中心天河2号等计算平台上完成，计算过程中得到了天津国家超算中心的有力配合。

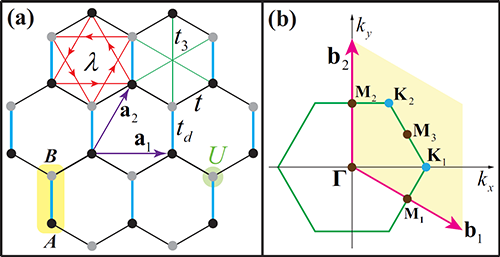
Fig. 1. （a）相互作用拓扑绝缘体中的 Kane-Mele-Hubbard 模型，系统具有最近临跃迁t，自旋轨道耦合lambda，三近邻跃迁 t3, 以及可以驱动系统进入能带绝缘体的最近临跃迁 td, 和库仑相互作用 U。（b）系统的布里渊区。

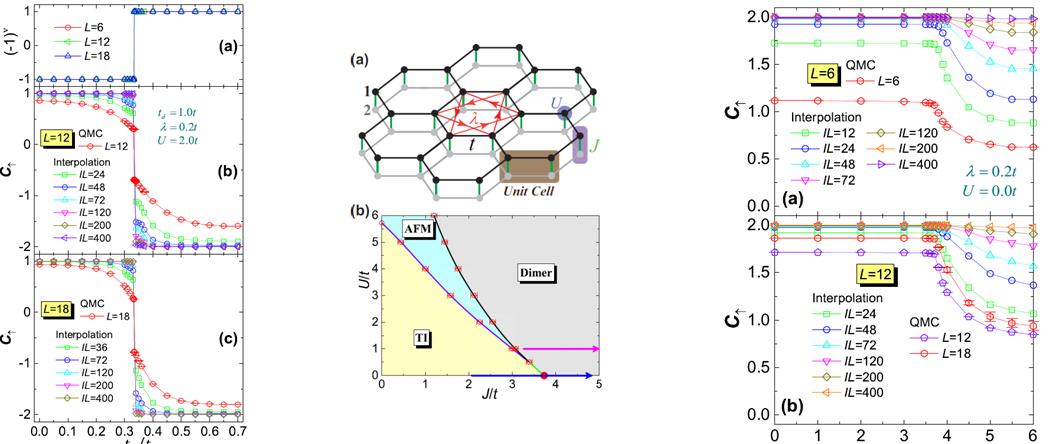
Fig. 2.(上图左图)由三近邻跃迁 t3/t 导致的系统拓扑相变，(a) 显示 Z2 不变量的变化，（b）,（c）显示系统自旋陈数的变化。在自旋陈数的变化中，L=12 和 L=18 的数据为有限尺度蒙特卡洛计算的结果，可以看到有限尺度系统的自旋陈数并没有整数化。而（b），（c）中的 Interpolation 结果为我们提出的周期函数差值所得的拓扑不变量，可以看到有限尺度效应被克服，系统自旋陈数整数化。

  Fig. 3. (上图中图)（a），（ b）相互作用拓扑绝缘体的双层 Kane-Mele-Hubbard-Heisenberg 模型，模型中层间电子的Heisenberg J 相互作用将会导致新型的相互作用驱动的拓扑相变，相变中没有对称性自发破缺，系统进入拓扑平庸的 dimer-singlet 直积态。这样的拓扑相变是用单粒子格林函数所构造的拓扑不变量所无法描述的（见Fig. 4），系统的拓扑信息要在集体激发中寻找。

Fig. 4. (上图右图)（a），（b）相互作用拓扑绝缘体双层 Kane-Mele-Hubbard-Heisenberg 模型中，层间电子的Heisenberg J 相互作用导致的拓扑相变，单粒子格林函数所构造的自旋陈数，在相变的左右两边都是整数化的，而在大 J 的 dimer-singlet 相中，系统的自旋霍尔电导率应该为零，这就说明了，在这个相互作用驱动的拓扑相变中，单粒子格林函数不能正确反应系统的自旋霍尔电导率。